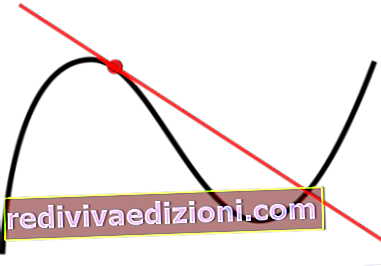
軌跡の定義
 解析幾何学の分野では、軌跡の概念には、与えられた方程式から座標軸上に作成された表面を指定または決定することが含まれます。これは、各数式に具体的なグラフィック表現があり、線、曲線、放物線、またはその他の図である可能性があることを意味します。
解析幾何学の分野では、軌跡の概念には、与えられた方程式から座標軸上に作成された表面を指定または決定することが含まれます。これは、各数式に具体的なグラフィック表現があり、線、曲線、放物線、またはその他の図である可能性があることを意味します。
他の数学的アイデアと同様に、軌跡の概念は抽象的なものです。数学的抽象化は、数と点という2つの基本単位に基づいています。1つ目は代数計算を行うために使用され、2つ目は幾何学的空間を理解するために使用されます。この意味で、軌跡は同じプロパティを共有するポイントのセットです。
この提案は、空間のより良い理解を可能にします
半径1メートルの円周を基準とすると、この幾何学的図形は、別の特定の点である円周の中心から等距離にある平面上の点の軌跡です。言い換えれば、軌跡を構成するすべての点の間の共通の距離は、円周の半径です。
解析幾何学は幾何学図形を研究しますが、これは数式によって行われます。これは、あらゆる種類の状況を表現したり、決定を下したり、現象を説明したり、特定の状況の基本的な特性を知ることができるツールです。最終的に、軌跡を表現する形状は、あらゆる種類の空間的現実を表現するのに役立ちます。
数学史における解析幾何学
ユークリッド幾何学は、紀元前3世紀にギリシャの数学者ユークリッドによって開発されました。Cと幾何学図形とその特性の研究に焦点を当てています。解析幾何学は、古典幾何学と代数の融合になります。
この分野の創設者は、17世紀のフランスの哲学者および数学者であるデカルトでした。彼の新しい幾何学のビジョンは、彼の有名な作品「The DiscourseofMethod」で開発されました。デカルトにとって、数学は適切に科学ではなく、科学自体を理解するための方法でした。数学では、物事の理由を説明することはすでに可能だったと言えます。
デカルト軸(デカルトという言葉はラテン語でデカルトの名前から来ています)は、解析幾何学の研究の伝統的な座標です。この意味で、代数的データ型の抽象表現は、放物線などの特定の画像で翻訳可能です。
解析幾何学は、代数曲線のセット(楕円、円周、放物線、双曲線、または双曲面)を扱います。
写真:Fotolia-mustgo