redivivaedizioni.com

派生語には2つの異なる用途がありますが、どちらも非常に繰り返し発生します。

一方では、化学の要請により、1つまたは複数の変換によって別の生成物から得られた生成物は誘導体と呼ばれます。たとえば、ガソリンは石油に由来します。

一方、数学などの別の科学的文脈では、導関数は、関数の増加と変数に対応する変数の増加の比率がゼロになる傾向がある場合の限界であることがわかります。

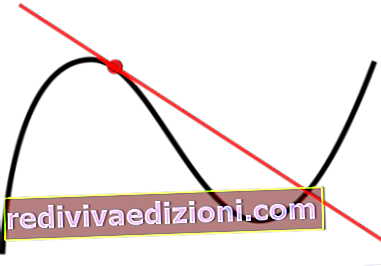
ある点での関数の導関数は、前述の点での接線の傾きの値を表し、関数が変化する係数を測定します。つまり、その係数の概念の数学的定式化が得られます。変化する。この係数は、2次元デカルト平面の軸を基準にした点で、関数がどれだけ速く成長するか、またはそれができない場合はどれだけ速く関数が減少するかを示します。

この概念は微積分の中心的な概念の1つですが、導関数は多くの用途がある概念です。たとえば、マグニチュードまたは状況のいずれかが発生する速度を測定する必要がある場合に適用されます。また、物理学、化学、生物学、または経済学や社会学などの社会科学の基本的な計算ツールでもあります。